MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [725]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

Radiação síncrotron, radiação sincrotrônica ^{(português brasileiro)} ou radiação sincrotrónica ^{(português europeu)} é a radiação eletromagnética emitida por uma partícula carregada (tipicamente elétrons ou pósitrons) movendo-se com velocidade relativística (ou seja, próxima à velocidade da luz) ao longo de uma trajetória curva, com raio de curvatura relativamente grande. Essa condição se aplica, em particular, para partículas circulando em aceleradores de elétrons ou pósitrons, cujo raio de curvatura é da de vários metros a dezenas de metros. O nome desta radiação deriva de um tipo específico de acelerador, o síncrotron de elétrons.^[1]

A radiação síncrotron também pode ter origem natural, sendo produzida por objetos astronômicos, como por exemplo remanescentes de supernovas (pulsares), quasares e núcleos de galáxias ativas. A radiação é produzida quando elétrons relativísticos espiralam ao longo dos campos magnéticos produzidos por estes objetos.^[2]^[3] Em astrofísica, uma partícula se movendo ao longo de geodésicas do espaço-tempo ao redor de buracos negros emite radiação síncrotron.^[4]^[5]^[6]^[7]

Jato energético da galáxia M87. A luz azul é causada por radiação síncrotron.

História

Os primeiros trabalhos teóricos sobre a radiação emitida por elétrons em órbitas circulares foram motivados pelas tentativas de se desenvolver modelos atômicos para explicar os espectros atômicos. Porém esses trabalhos foram tornados obsoletos pelo modelo atômico de Bohr. Posteriormente, no início dos anos de 1940, o interesse no problema foi reavivado com o advento de aceleradores de elétrons circulares como o bétatron, e a constatação de que essa radiação emitida era um fator limitante na energia máxima que poderia ser alcançada com esses aceleradores.^[1]

O tratamento teórico dessa radiação foi desenvolvido por várias pessoas, entre elas destacam-se: J. Schwinger e D. Ivanenko, A.A. Solokov e I.M.Ternov^[1], além de D.H.Tomboulian e P.L. Hartman, Godwin e Jackson.^[8]

Do ponto de vista experimental, a radiação emitida por um acelerador síncrotron foi observada em 1946 nos laboratórios da General Electric. Essa observação foi feita com um síncrotron de elétrons de 70 MeV localizado em Schenectady.^[1]

Até o final dos anos de 1950, o estudo da radiação síncrotron foi motivada principalmente pelo seu aspecto negativo na tecnologia de aceleradores. Mas em 1956, um artigo de Tomboulian e Hartman, iniciou uma revolução em termos de utilização dessa radiação, eles utilizaram a radiação para estudos de espectroscopia de absorção no ultravioleta distante e raios X.^[1]

Potência irradiada

Como ponto de partida, pode-se tomar a expressão para a potência irradiada por uma carga acelerada não relativística, também conhecida como fórmula de Larmor:^[8]^[9]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$P={\frac {2}{3}}{\frac {e^{2}}{m^{2}c^{3}}}{\Bigl (}{dp \over dt}{\Bigr )}^{2}$ (1) em unidades cgs.

$�$ = carga elétrica;

$�$ = massa;

$�$ = velocidade da luz;

$�$ = momento.

Para uma carga em movimento circular com o raio da órbita valendo $\rho$ , temos que a potência irradiada será:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$P={\frac {2}{3}}{\frac {e^{2}c}{\rho ^{2}}}\beta ^{4}\gamma ^{4}$ (2)

$\rho$ = raio da órbita;

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$\beta ={\frac {v}{c}}$

$\gamma ={\frac {1}{\sqrt {1-(v^{2}/c^{2})}}}$

Além disso, pode-se mostrar que a energia perdida (ΔE) a cada revolução é:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$\Delta E={\frac {4\pi }{3}}{\frac {e^{2}}{\rho }}\beta ^{3}\gamma ^{4}$ (3)

Para partículas com energias relativísticas, $\beta$ $\approxeq$ 1, assim a equação (2) nos diz que a potência irradiada é inversamente proporcional a $\rho$ ² e diretamente proporcional a $\gamma$ ⁴.

Sendo que $\gamma$ (fator de Lorentz) pode ser escrito como:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$\gamma ={\frac {E_{total}}{E_{repouso}}}$

A $E_{repouso}$ do elétron é 0,511 MeV e a do próton é 938 MeV. Assim, para a mesma energia total e o mesmo raio, pode-se notar que partículas pesadas como o próton, produzem uma intensidade de radiação síncrotron desprezível quando comparada com a que é produzida por elétrons.

Na Física, o vetor de Poynting representa a densidade direcional do fluxo de energia (a quantidade de energia transferida por unidade de área, em watts por metro quadrado (W·m⁻²)) de um campo eletromagnético. Foi nomeado em homenagem ao seu descobridor John Henry Poynting. Oliver Heaviside e Nikolay Umov independentemente co-descobriram o vetor de Poynting.

Definição

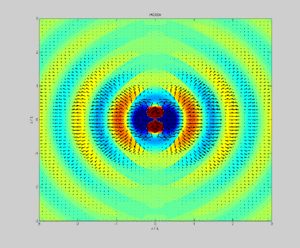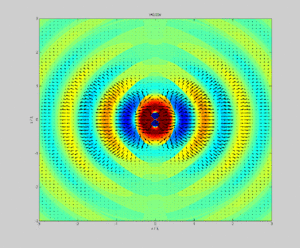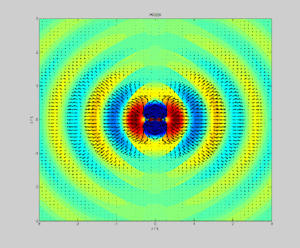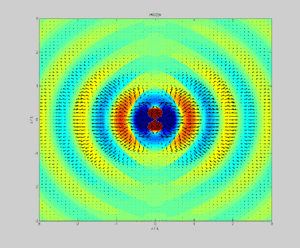
Radiação de um dipolo disposto verticalmente na página mostrando a intensidade do campo elétrico (cores) e o vetor de Poynting (setas) no plano da página.

Nos trabalhos originais de Poynting e em muitos livros texto, é usualmente denotado por S ou N, e definido como:^[1]^[2]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {S} =\mathbf {E} \times \mathbf {H} ,

a qual é comumente chamada de forma de Abraham; onde E é o campo elétrico e H o campo magnético.^[3]^[4] (Todas as letras em negrito representam vetores.)

Ocasionalmente uma definição alternativa em termos de campo elétrico E e a densidade de fluxo magnético B é usada. É sempre possível combinar o campo de deslocamento D com a densidade de fluxo magnético B para ter a forma Minkowski do vetor de Poynting, ou usar D e H para construir outro.^[5] A escolha tem sido controversa: Pfeifer et al.^[6] e resume a longa disputa centenária entre proponentes das formas de Abraham e Minkowski.

O vetor de Poynting representa o caso particular do vetor do fluxo de energia para energia eletromagnética. Entretanto, qualquer tipo de energia tem sua direção de movimento no espaço, assim como sua densidade, então os vetores de fluxo podem ser definidos para outros tipos de energia também, exemplo, para energia mecânica. O vetor Umov-Poynting ^[7] descoberto por Nikolay Umov em 1874 descreve o fluxo de energia em médias elásticas e líquidas numa visão completamente generalizada.

Interpretação

O vetor de Poynting aparece no teorema de Poynting (veja este artigo para a dedução do teorema e do vetor), uma lei de conservação de energia,^[4]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\frac {\partial u}{\partial t}}=-\mathbf {\nabla } \cdot \mathbf {S} -\mathbf {J} _{f}\cdot \mathbf {E} ,

onde J_f é a densidade de corrente das cargas livres e u é a densidade de energia eletromagnética,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

u={\frac {1}{2}}\left(\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} \right)

onde B é a densidade de fluxo magnético e D o campo de deslocamento elétrico.

O primeiro termo do lado direito representa a rede do fluxo de energia eletromagnética em um volume pequeno, enquanto o segundo termo representa a porção subtraída do trabalho executado pelas correntes elétricas livres que não são necessariamente convertidas em energia eletromagnética (dissipação, calor). Nesta definição, correntes elétricas ligadas não são incluídas neste termo, e em vez disso contribuem para S e u.

Note que u só pode ser dado se for linear, não dispersiva e materiais uniformes são envolvidos, i.e., se as relações constitutivas podem ser escritas como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {D} =\varepsilon \mathbf {E} \,\quad \mathbf {H} =\mathbf {B} /\mu

onde ε e μ são constantes (as quais dependem do material onde a energia flui), chamadas de permissividade e permeabilidade, respectivamente, do material.^[4]

Isto praticamente limita o teorema de Poynting na sua forma para campos no vácuo. Uma generalização para materiais dispersivos é possível sobre certas circunstâncias no custo de termos adicionais e na perda de suas interpretações físicas claras.^[4]

O vetor de Poynting é usualmente interpretado como fluxo de energia, mas isso só é estritamente correto para radiação eletromagnética. O caso mais geral é descrito pelo teorema de Poynting descrito acima, onde isto ocorre como divergência, que significa que só pode descrever a mudança da densidade de energia no espaço, ao invés de fluxo.

Invariância à adição de uma onda de um campo

Visto que o vetor de Poynting somente ocorre no teorema de Poynting como divergência ∇ • S, o vetor de Poynting S é arbitrariamente na medida em que se pode adicionar rotações de um campo F para S,^[4]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {S} '=\mathbf {S} +\nabla \times \mathbf {F} \,\Rightarrow \,\nabla \cdot \mathbf {S} '=\nabla \cdot \mathbf {S} \,,

visto que a divergência do termo da onda é zero: ∇ • (∇ × F) = 0 para um campo arbitrário F. Fazer isso não é comum ou útil embora, e vai levar a inconsistências na descrição relativista do campo eletromagnético nos termos do tensor de energia-momento.

Formulação em termos de campos microscópicos

Em alguns casos, pode ser mais apropriado em definir o vetor de Poynting S como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {S} ={\frac {1}{\mu _{0}}}\mathbf {E} \times \mathbf {B} ,

onde μ₀ é a constante magnética. Pode ser deduzido diretamente das equações de Maxwell em termos de carga e corrente total e da lei da força de Lorentz somente.

A forma correspondente do teorema de Poynting é

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\frac {\partial u}{\partial t}}+\nabla \cdot \mathbf {S} =-\mathbf {J} \cdot \mathbf {E} ,

onde J é a densidade de corrente total e a densidade de energia u é

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

u={\frac {1}{2}}\left(\varepsilon _{0}\mathbf {E} ^{2}+{\frac {1}{\mu _{0}}}\mathbf {B} ^{2}\right)

onde ε₀ é a constante elétrica.

As duas definições alternativas do vetor de Poynting são equivalentes no vácuo ou em metais não magnéticos, onde B = μ₀ H. Em todos outros casos, eles diferem nisso

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {S} ={\frac {1}{\mu _{0}}}\mathbf {E} \times \mathbf {B} ,

e a correspondente u é puramente radiativa, visto que o termo de dissipação, (−J • E) cobre a corrente total, enquanto a definição em termos de H tem contribuições das correntes amarradas que falta então o termo de dissipação.^[8]

Visto que somente os campos microscópicos E e B são necessários na dedução de

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {S} ={\frac {1}{\mu _{0}}}\mathbf {E} \times \mathbf {B} ,

suposições sobre qualquer material possivelmente presente pode ser completamente evitada, e o vetor de Poynting assim como o teorema nesta definição são universalmente válidos, no vácuo e qualquer tipo de material. Isto é especialmente verdadeiro para a densidade de energia eletromagnética, em contraste para o caso acima.^[8]

${\vec {w}}={\vec {v}}-{\vec {u}}$

e que:

$w_{x}=v_{x}-u_{x}$

assim como:

$w_{y}=v_{y}-u_{y}.$

Logo temos que, dados dois vetores:

${\vec {v}},{\vec {u}}$

a sua subtração resulta em:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

${\vec {w}}=\langle v_{x}-u_{x},v_{y}-u_{y}\rangle$

Tempo médio do vetor de Poynting

Para campos eletromagnéticos de funções periódicas senoide, a média do fluxo de energia por unidade de tempo é muitas vezes mais útil, e pode ser encontrando tratando os campos elétricos e magnéticos como vetores complexos e segue (asterisco * denota o conjugado):

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\begin{aligned}\mathbf {S} &=\mathbf {E} \times \mathbf {H} \\&=\mathrm {Re} \left(\mathbf {\widetilde {E}} \right)\times \mathrm {Re} \left(\mathbf {\widetilde {H}} \right)\\&=\mathrm {Re} \left(\mathbf {E_{c}} e^{j\omega t}\right)\times \mathrm {Re} \left(\mathbf {H_{c}} e^{j\omega t}\right)\\&={\frac {1}{2}}\left(\mathbf {E_{c}} e^{j\omega t}+\mathbf {E_{c}} ^{*}e^{-j\omega t}\right)\times {\frac {1}{2}}\left(\mathbf {H_{c}} e^{j\omega t}+\mathbf {H_{c}} ^{*}e^{-j\omega t}\right)\\&={\frac {1}{4}}\left(\mathbf {E_{c}} \times \mathbf {H_{c}} ^{*}+\mathbf {E_{c}} ^{*}\times \mathbf {H_{c}} +\mathbf {E_{c}} \times \mathbf {H_{c}} e^{2j\omega t}+\mathbf {E_{c}} ^{*}\times \mathbf {H_{c}} ^{*}e^{-2j\omega t}\right)\\&={\frac {1}{4}}\left(\mathbf {E_{c}} \times \mathbf {H_{c}} ^{*}+\left(\mathbf {E_{c}} \times \mathbf {H_{c}} ^{*}\right)^{*}+\mathbf {E_{c}} \times \mathbf {H_{c}} e^{2j\omega t}+\left(\mathbf {E_{c}} \times \mathbf {H_{c}} e^{2j\omega t}\right)^{*}\right)\\&={\frac {1}{2}}\mathrm {Re} \left(\mathbf {E_{c}} \times \mathbf {H_{c}} ^{*}\right)+{\frac {1}{2}}\mathrm {Re} \left(\mathbf {E_{c}} \times \mathbf {H_{c}} e^{2j\omega t}\right).\end{aligned}}

A média sobre o tempo é dado como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\langle \mathbf {S} \rangle ={\frac {1}{T}}\int _{0}^{T}\mathbf {S} (t)dt={\frac {1}{T}}\int _{0}^{T}\left[{\frac {1}{2}}\mathrm {Re} \left(\mathbf {E_{c}} \times \mathbf {H_{c}} ^{*}\right)+{\frac {1}{2}}\mathrm {Re} \left(\mathbf {E_{c}} \times \mathbf {H_{c}} e^{2j\omega t}\right)\right]dt.

O segundo termo é uma curva senoidal

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathrm {Re} \left(e^{2j\omega t}\right)=\cos 2\omega t

e sua média é zero, dando

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\langle \mathbf {S} \rangle ={\frac {1}{2}}\mathrm {Re} \left(\mathbf {E_{c}} \times \mathbf {H_{c}} ^{*}\right)={\frac {1}{2}}\mathrm {Re} \left(\left[\mathbf {E_{c}} e^{j\omega t}\right]\times \left[\mathbf {H_{c}} ^{*}e^{-j\omega t}\right]\right)={\frac {1}{2}}\mathrm {Re} \left(\mathbf {\widetilde {E}} \times \mathbf {\widetilde {H}} ^{*}\right).

Pesquisar este blog

MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [725]

História

Potência irradiada

Definição

Interpretação

Invariância à adição de uma onda de um campo

Formulação em termos de campos microscópicos

Tempo médio do vetor de Poynting

Comentários

Postar um comentário

Postagens mais visitadas deste blog